Analýza termodynamických jevů v potrubních sítích – numerický model teplotního pole v okolí teplárenského potrubí – 2. část
Pokračování série o vyhodnocování tepelných ztrát teplárenských sítí se věnuje numerickému modelování teplotního pole v bezprostředním i vzdálenějším okolí povrchu potrubní izolace.
© Fotolia.com
První část článku naleznete ZDE.
V souvislosti s obtížností řešení analytickými metodami a především v souvislosti s nepřesností jejich výsledků zejména v méně typických, přesto nikoliv vzácných provozních režimech, se nabízí jako vhodná cesta pro popis celého děje vytvoření dvourozměrného modelu teplotního pole vznikající během provozu kolem teplárenského potrubí. Předložený numerický model využívá růstu výpočetních kapacit v posledních letech tak, že velikost jednoho segmentu výpočtové mřížky je 10 × 10 mm, což je, např. pro stanovení vhodnosti umístění jiné potrubní sítě, či kabelu, v okolí horkovodu, jemnost již dostatečná. Vzniklý numerický model je připravován, na rozdíl od podstatné části analytických metod, pro výpočet plného rozsahu možných provozních podmínek horkovodu a klimatických podmínek na zemském povrchu.
2.2. Popis numerické metody
Pro obdélníkovou oblast v pravoúhlé soustavě, v rozsahu os x = (0 až 6000) mm a y = (0 až 4000) mm ohraničené shora a zdola okrajovými podmínkami 1. typu, jsou známé konkrétní hodnoty teploty na spodní i dolní hranici výpočtového pole, kde t = konst. Výpočtové teplotní pole je ohraničené zleva a zprava okrajovými podmínkami druhého typu, tedy nulovým teplotním gradientem, a z něj plynoucím nulovým tepelným tokem ve směrech do a z teplotního pole v x-ové souřadnici, tedy 
(viz Obrázek 2.2.1.). V této oblasti lze vyřešit parabolickou diferenciální rovnici v podobě
(2.2.1.)
s okrajovými podmínkami danými fyzikálním modelem teplotního pole a s počáteční hodnotou teploty uvnitř teplotního pole, volenou jako zcela minimální, jaká se v dané oblasti může vyskytovat. Pro oblast ČR lze předpokládat tmin = (−30 °C).
Fourierova rovnice vedení tepla 
je parciální rovnice 2. řádu, parabolického typu. Pro rovnici parabolického typu platí, že poruchy (změna počáteční podmínky) se šíří nekonečnou rychlostí.
V případě sdílení tepla je tato rovnice rozšířena o fyzikální parametr teplotní vodivosti (teplotní difusivity)
,
(2.2.2.)
a tedy
(2.2.3.)
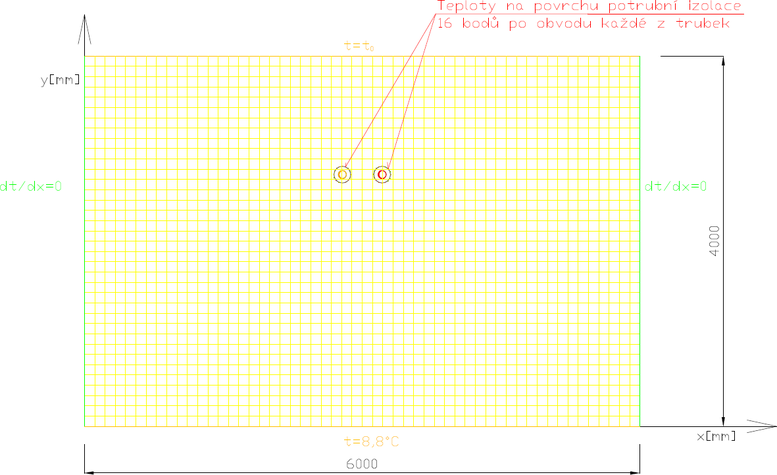
Obrázek 2.2.1. – Okrajové podmínky numerického výpočtu zaměřeného na získání mapy teplotního pole v okolí dvoutrubního horkovodu
Pro praktickou funkčnost výpočtu je nutno zabývat se i kritériem ustáleného stavu. Pro účely tohoto výpočtu volíme 
.
Pro numerické řešení rovnice je zvolena metoda sítí. Tato metoda spočívá v tom, že prostor řešení x, y a τ je rozdělen rovnoměrně rozloženými body 
, kde Δx, Δy jsou kroky v příslušné prostorové souřadnici. Hodnota Δτ je krok v časové souřadnici. Uvažováním postupu výpočtu dle těchto kroků je získána síť bodů 
, ve kterých je nalezeno numerické řešení s příslušnou dovolenou chybou. Numerické řešení tedy není totožné s analytickým – vždy dochází k rozdílu mezi analyticky a numericky získanou hodnotou v identickém bodě (např. ve výpočtovém uzlu) teplotního pole.
Na základě srovnání vypočtených hodnot teploty v jednotlivých bodech teplotního pole, a hodnot uvnitř tohoto pole naměřených, bylo, vzhledem k odchylkám mezi měřením a numerickým modelem až o 8 K, patrné, že přístup, předpokládající konstantní tepelnou vodivost λE ≅ konstanta, je pro řešení této úlohy nedostačující. Z tohoto důvodu byla pro zpřesnění teplotního pole vytvořením matice x ‧ y mapující teplotní vodivost a ve všech uzlových bodech, opět využita numerická metoda na základě řešení parciální diferenciální rovnice
,
(2.2.4.)
při okrajových podmínkách 1. typu na všech čtyřech stranách posuzovaného pole teplotní vodivosti, kde, vzhledem k převaze hlíny nad pískem v obsahu zeminy, je teplotní vodivost a = aEmax. Tato maximální teplotní vodivost odpovídá původní teplotní vodivosti rostlé zeminy v lokalitě, tedy bez dodatečně přimíchaného písku. Toto pole teplotní vodivosti je, kromě svých okrajových podmínek, determinováno i hodnotami tepelné vodivosti získanými měřením v okolí potrubní dvojice a z nich vypočtených hodnot vodivosti teplotní. Naopak, v bezprostředním okolí potrubní konstrukce, kde v zásypové hmotě převládá (poměrně suchý) písek, je předpokládána teplotní vodivost a = aEmin.
2.2.1. Numerické schéma
Je použito explicitní numerické schéma 1. řádu přesnosti v čase a 2. řádu v prostoru.
Pro explicitní schéma v bodě [xi, yj, τn] nahradíme rozdíl teplot centrální derivací, a tím rovnice 2.2.4. přechází ve tvar
(2.2.5.)
a pro získání hodnoty teplotní vodivosti 
pak platí
.
(2.2.6.)
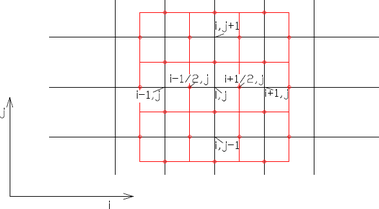
Obrázek 2.2.2. – Posuzovaná oblast pro určení teplotní vodivosti v polovině mezi jednotlivými uzly výpočtové sítě teploty v teplotním polive vztahu k bodu i, j. Teplotní vodivost je definována výpočtem na hranici červeně vyznačených čtverců.
Pro získání hodnoty teploty, v každém uzlovém bodu teplotního pole, je třeba započíst tepelně technické vlastnosti materiálu, ve kterém k vedení tepla dochází, tedy jeho hustoty, tepelné vodivosti a měrné tepelné kapacity (cP ≈ cv) prostřednictvím teplotní vodivosti dle rovnice (2.2.2.), a to v oblasti mezi každými dvěma teplotními uzly, tedy cílem je výpočet teploty při uvažování teplotní vodivosti 
a 
a 
a 
tak, aby byl stále dodržen konzervativní princip zachování tepelné energie, viz Obrázek 2.2.2., kde je vždy oblast posuzované teplotní vodivosti v okolí uzlových bodů vyznačena červeným čtvercem ohraničeným přímkami v polovině vzdálenosti mezi uzlovými body výpočtu.
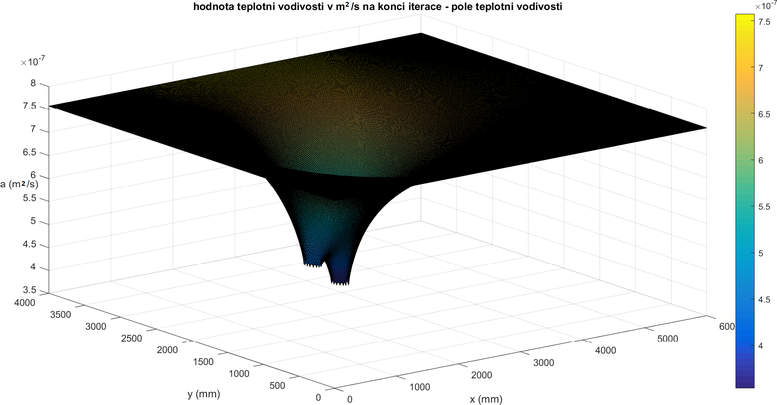
Průběh iterací při výpočtu teplotní vodivosti je patrný z Obrázku 2.2.3. a výsledný průběh teplotní vodivosti v numerickém modelu je patrný z Obrázku 2.2.4.
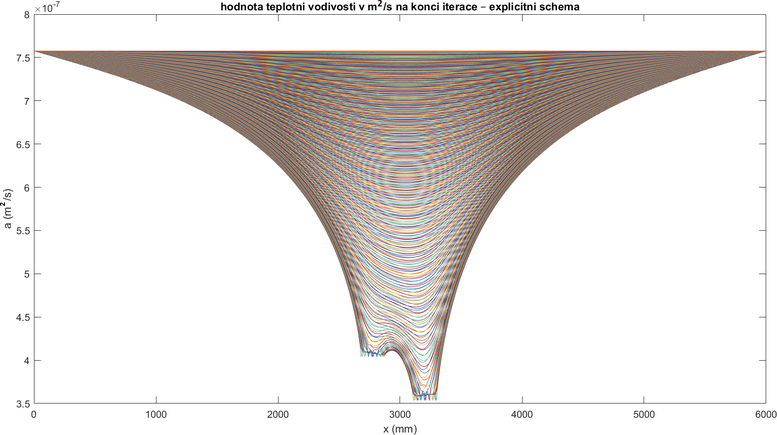
Obrázek 2.2.3. – Průběh iterací (konvergence výpočtu) při modelování průběhu teplotní vodivosti uvnitř modelovaného teplotního pole
Obrázek 2.2.4. – Teplotní vodivost posuzovaného teplotního pole v numerickém modelu
Pro výpočet teploty, v závislosti na proměnné teplotní vodivosti teplotního pole, lze využít Fourrierovu rovnici vedení tepla ve tvaru
.
(2.2.7.)
Pokud označíme výraz 
jako A a výraz 
jako B, pak pro řešené teplotní pole platí
(2.2.8.)
Uvedený vztah však není možno použít v krajních hodnotách teplotního pole, protože např. pro výpočet teploty 
by byla třeba neznámá hodnota 
, která je, i vzhledem k charakteru okrajových podmínek na levém a pravém okraji teplotního pole, předem neznámá. Stejně tak i na pravém okraji teplotního pole je třeba zajímat se o hodnotu teploty ve všech výpočtových uzlech se souřadnicí imax, tedy 
. Z těchto důvodů je nutno pro levou a pravou stranu teplotního pole hodnoty 
na levém, a 
na pravém okraji výpočtového pole dopočítat, a to na straně levé, z hodnot následujících, tj. 
a 
a na straně pravé z teplot předcházejících předmětné hodnotě, tj. z hodnot 
a z 
.
Vybraná explicitní metoda je podmíněně stabilní, což značí, že časový krok Δτ je v zájmu stability shora omezený, a to v závislosti na vzdálenosti výpočtových uzlů Δx a Δy. Podmínka stability je, dle [6]
(2.2.9.)
kde aEmax je nejvyšší hodnota teplotní vodivosti zemního zásypu.
Z hlediska požadované přesnosti mapy teplotního pole byla, jako vhodná velikost dělení tohoto pole, volena obvyklá technicky dosažitelná přesnost ukládání inženýrských sítí v zemi (±5 mm). Na základě této možné odchylky polohy potrubí v prostoru byla zvolena výpočtová síť o vzdálenosti uzlů Δx = Δy = 10 mm.
Za ustálený stav je v tomto výpočtu pokládána možná odchylka mezi jednotlivými hodnotami přiblížení výsledné teploty = absolutní hodnota největšího rozdílu mezi vypočtenými hodnotami v kterémkoliv z uzlů řešeného teplotního pole.
2.3. Výsledky numerického řešení teplotního pole okolí potrubí zasypaného v zemním zásypu
Uvedené numerické schéma bylo použito k vytvoření programu, jehož hlavními výstupními hodnotami jsou teploty ve všech uzlech výpočtového pole vypočtené na základě hodnot teplot naměřených na izolačním plášti obou potrubí, na teplotě povrchu země a stabilní teplotě v dostatečné hloubce pod povrchem země. Složení teplotního pole, vzniklého numerickou cestou, je, pro jednotlivé provozní okamžiky v topném období, patrné z Obrázků 2.3.1 až 2.3.3.
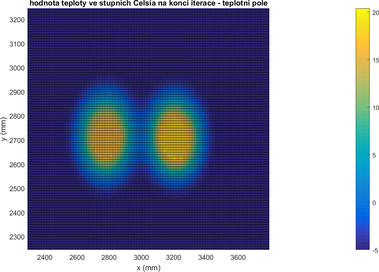
Obrázek 2.3.1. – Obecný detail hodnoceného teplotního pole (bezprostřední okolí potrubí) v numerickém modelu – vpravo přívodní linie, vlevo vratná linie. Souřadný systém dle obrázku 2.1.5.
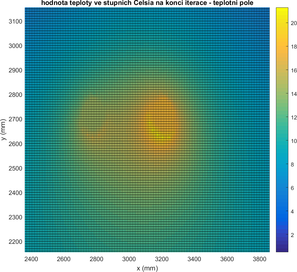
Obrázek 2.3.2. – Detail hodnoceného teplotního pole (v blízkém okolí potrubí) pro den 30. prosince 2014 12:05 h v numerickém modelu – vpravo je zobrazena přívodní linie, vlevo vratná linie horkovodu. Souřadný systém dle obrázku 2.1.5.
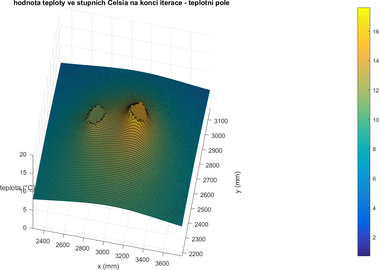
Obrázek 2.3.3. – Detail hodnoceného teplotního pole (v blízkém okolí potrubí) pro 5. únor 2015 16:36 h v numerickém modelu – vpravo je zobrazena přívodní linie, vlevo vratná linie horkovodu. Souřadný systém dle obrázku 2.1.5.
Průběh teploty v teplotním poli, pro období mimo topnou sezonu, je v numerickém modelu patrný z Obrázků 2.3.4 a 2.3.5. Zde je patrné vysoké prohřátí zásypové zeminy mezi bezprostředním okolím potrubí a povrchem země, kdy teplota v celé této oblasti trvale přesahuje 20 °C.
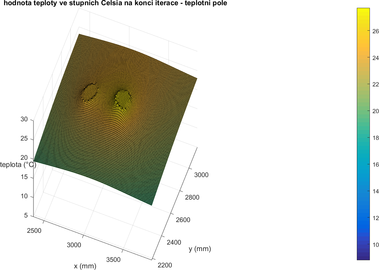
Obrázek 2.3.4. – Detail hodnoceného teplotního pole (v blízkém okolí potrubí) pro 27. srpen 2015 14:11 h v numerickém modelu – vpravo je zobrazena přívodní linie, vlevo vratná linie horkovodu. Souřadný systém dle obrázku 2.1.5.
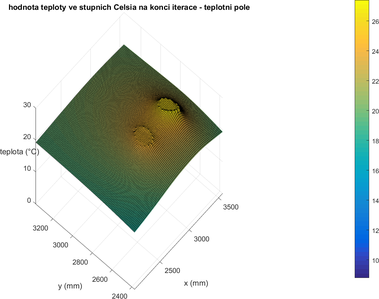
Obrázek 2.3.5. – Detail hodnoceného teplotního pole (v blízkém okolí potrubí) pro 8. září 2015 15:02 h v numerickém modelu – vpravo je zobrazena přívodní linie, vlevo vratná linie horkovodu. Souřadný systém dle obrázku 2.1.5.
3. Hodnocení přesnosti numerického modelu
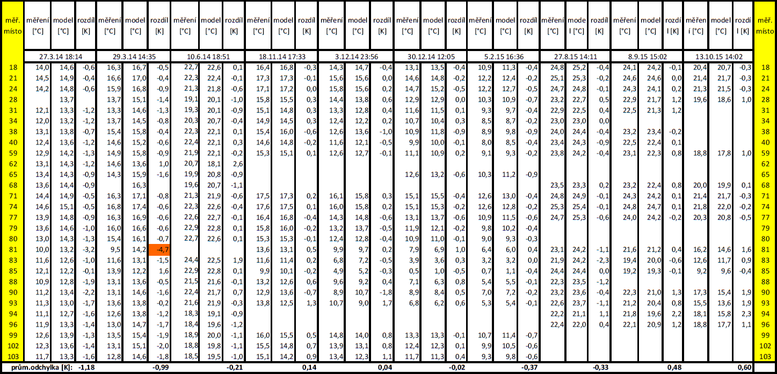
Pro posouzení kvality numerického modelu teplotního pole v okolí potrubní konstrukce bylo využito srovnání více naměřených provozních stavů (vždy minimálně jeden z každé měřící periody) s hodnotami získanými pro stejné podmínky z matematického modelu (viz Tabulka 1). Pro tyto hodnoty byl numerický model validován. Validace modelu s využitím naměřených teplot povrchů potrubní konstrukce byla úspěšná, model v oblasti instalační rýhy (profilu původního montážního výkopu horkovodu) vykazoval průměrnou velikost odchylky od měření minus 0,25 K a nevykazoval v žádném místě měřeného teplotního pole odchylku mezi měřením a numerickým modelem v absolutní hodnotě větší než 4,7 K (v Tabulce 1 vyznačeno červenou barvou), což vzhledem k obtížně predikovatelné homogenitě zásypu lze považovat za vyhovující. Naprostá většina hodnot odchylek modelu od měření, jak je patrné z Tabulky 1, je v oblasti od 0 do 2 K. Jak je patrné, model vykazuje poměrně značnou shodu s naměřenými hodnotami, a to i v případě letních měření, kdy se mění poměr vlivu jednotlivých zdrojů tepla v teplotním poli směrem od tepelného toku z horkovodu ve prospěch slunečního záření.
4. Aplikace numerické modelu teplotního pole pro posouzení vhodnosti souběhu horkovodu s dalšími inženýrskými sítěmi
V souvislosti se zvyšováním hustoty inženýrských sítí v intravilánech měst i podél liniových dopravních staveb, je nutno řešit problematiku vhodnosti či nevhodnosti souběhu mezi teplovodní či horkovodní potrubní trasou, příp. trasou dálkového chlazení, ve vztahu k podélně vedenému (souběhem) nebo křižujícímu vodovodnímu řadu. Týž problém, a s ještě nebezpečnějšími důsledky v případě špatného řešení, se týká i souběhů a křížení horkovodů se silovými elektrickými kabely vysokých napětí, jejichž elektroizolační pláště mohou být poškozovány tepelným působením – teplem, vedeným zemním zásypem v okolí funkčních horkovodů. Podobné problémy vyvstávají i u rozvodů chladících látek, a to ve vztahu ke křehnutí izolací elektro kabelů v jejich bezprostředním okolí. Tento problém v technické rovině řeší v ČR stále platná, a průběžně aktualizovaná, technická norma ČSN 73 6005, která však není závazná, a vzhledem k aktuální hustotě inženýrských sítí ve většině měst, není její respektování, či jejích dalších evropských ekvivalentů, ve většině případů vůbec možné.
Z tohoto důvodu je třeba řešit vždy konkrétní případ umístění a vzájemné polohy podzemních sítí uvnitř teplotního pole, vzniklého v souvislosti s vedením tepla z/do potrubí.
Vypracovaný numerický model postihuje toto řešení vytvořením teplotního pole, ze kterého je možno, po zadání souřadnic vyšetřovaného místa, a hodnot povrchové teploty na povrchu izolačního pláště, získat konkrétní teplotu v místě lokace souběžné či křížící se inženýrské sítě.
Obecnou podmínkou plné funkčnosti předloženého numerického modelu je, že vyšetřovaný bod, nebo soustava bodů, nejsou samy významným zdrojem tepelné energie. V situaci, kdy je předmětem zkoumání možnosti umístění např. elektrického kabelu do okolí horkovodního potrubí, je zde cestou k posouzení „významnosti“ kabelu, jako samostatného tepelného zdroje, poměr mezi topným výkonem tohoto kabelu (W/m), oproti tepelné ztrátě horkovodního potrubí (W/m) v jehož zóně vlivu se má tento kabel vyskytovat. V takovýchto případech je možno opět s úspěchem použít superpozičního principu, popsaného v předchozích článcích tohoto cyklu.
Tabulka 1 – Rozdíl mezi teplotou uvnitř teplotního pole naměřenou v konkrétním měřícím místě a teplotou vypočtenou pro toto místo v numerickém modelu, vytvořeném v programu MATLAB.
5. Návrh další diskuse
Předložený numerický model a způsob validace jednotlivých výsledků měřením má svá omezení, spočívající především ve výpočtové kapacitě a správném stanovení okrajových podmínek modelu. Podstatnou otázkou zde je, z hlediska této validace, správné stanovení teploty, ohraničující z horní strany mapované teplotní pole. Předložený model pracuje s hodnotou povrchové tenké vrstvy zeminy, která je v experimentu trvale měřena a která do značné míry tlumí výkyvy skutečné povrchové teploty, zcela závislé na okamžitém slunečním svitu a rychlosti proudění vzduchu, případně i stavu vzrůstu vegetačního krytí nad horkovodní potrubní trasou, event. i aktivit nad předmětnou trasou probíhajících. Z tohoto pohledu se jeví jako pro model podstatně jistější okrajové podmínky na levé a pravé straně, a ještě více na spodním okraji teplotního pole, jejichž přesnost může být bez závislosti na posuzované lokalitě velmi značná a v budoucnu, při nárůstu výpočtové kapacity, je možno zvětšením (šířkou i výškou) výpočtové numerické sítě, případně i její větší hustotou, dosáhnout dalšího zpřesnění výpočtu teplot v každém ze sledovaných bodů.
6. Získané poznatky
Hlavním přínosem provedených prací je numerický model teplotního pole v semihomogenním prostoru, vzniklém v okolí funkčního horkovodu v běžných technických podmínkách teplárenského provozu a jeho úspěšná validace na základě měření. Podstatným poznatkem pro práci v tomto oboru jsou naměřené odchylky v jednotlivých bodech sítě numerického modelu od naměřených hodnot, popsané pro jednotlivá roční období a s nimi souvisejícími provozními parametry horkovodů. Stanovení okrajových podmínek modelu na základě analytických řešení chování zdroje tepla v polonekonečném prostoru, i na základě naměřených hodnot, je rovněž poznatkem, plynoucím z postupu práce na tvorbě modelu.
Hranicemi předložených poznatků jsou omezení daná podmínkami realizovaného experimentu, tedy, především v souvislosti s provedenou validací, kdy lze konstatovat pouze tolik, že existuje velmi vysoká pravděpodobnost funkčnosti numerického modelu za podmínek shodných, či blízkých, podmínkám měřeným. Z tohoto pohledu se může jevit aplikovatelnost modelu jako omezená. Avšak, vzhledem k tomu, že stavební řešení teplárenských potrubí jsou v současnosti normalizována právě ve tvaru blízkém konfiguraci potrubí, použitého pro experiment, není uvedené omezení z tohoto pohledu příliš významné. Přesto, z pohledu dalšího výzkumu, je třeba vzít v úvahu, že validace modelu proběhla na standardní teplárenské trase, byť za různých provozních podmínek a nikoliv za speciálně připravených podmínek, které mohou, např. hlubokým zámrzem povrchové vrstvy, či dlouhodobým odstavením horkovodu z provozu, funkčnost modelu omezit. Podobně může být přesnost modelu omezena při výrazné změně skladby zásypové zeminy, či při vzniku možných extrémů počasí na horní hranici vyšetřovaného teplotního pole.
Z tohoto důvodu je při další práci možno pokračovat tvorbou numerického modelu, postihujícího jak dynamické účinky (pro jehož realizaci jsou již uvnitř stávající numerického modelu vytvořeny podmínky), tak případně i nelinearity ve vlastnostech vyšetřovaného teplotního pole, zejména s ohledem na změnu vlastností zásypu.
Seznam použité literatury
- JANNA, W. S.; Engineering heat transfer 3rd edition, Broken Sound Parkway NW: CRC Press, Taylor & Francis Group, 2009, ISBN 978-1-4200-7202-0.
- BOHM, B.; KRISTJANSSON, H.; Single, twin and triple buried heating pipes: on potential savings in heat losses and costs. International Journal of Energy Research, strany 1301–1312, 18. července 2005, Wiley InterScience, DOI: 10.1002/er.1118, dostupné z www.interscience.wiley.com.
- PERPAR, M. a kolektiv; Soil thermal conductivity prediction for district heating pre-insulated pipeline in operation, Energy, 2012, vol. 44, číslo 1, str. 197–210, ISSN 0360-5442, dostupné z
http://www.sciencedirect.com/science/article/pii/S0360544212004884. - KNEER, A.; WIRTZ, M.; Development of an alternative cooling system (earth heat exchanger) for inverters of a solar plant, příspěvek z konference Star European conference, 22.–23. března 2011, Noordvik, dostupný z
http://www.tinnit.de/cms/download.php?cat=30_Umwelttechnik&file=Starconference_2011_earthcooling_tinnit.pdf - PROKOP, J.; Tepelné izolace v tepelné technice, vydavatelství ČVUT, Praha, 1992, 144 str. ISBN 80-01-00888-6.
- JALURIA, Y.; TORRANCE, K. E.; Computational heat transfer: series in computational and physical processes in mechanics and thermal sciences. 2. vydání, New York, Taylor & Francis, 2003. 2. vydání, ISBN 1-56032-477-5.
Another of several articles dealing with thermal losses evaluation of heating networks is focused on the numerical modeling of the temperature field in the immediate and distant surroundings of the pipe insulation surface. In connection with the difficulty of solving the analytical methods and in particular with the inaccuracy of their results, especially in less typical but not rare operating regimes, a two-dimensional model of the thermal field generated during the operation around the heating pipeline is offered as a suitable path for describing the whole process. The presented numerical model uses the growth of computational capacities in recent years, so that the size of one segment of the calculation grid is 10 x 10mm, which is, for example, to determine the suitability of the location of another pipe network or cable, near the hot-water pipe, the fineness is already sufficient. The resulting numerical model is being prepared, unlike a substantial part of the analytical methods, to calculate the full range of possible operating conditions of the hot-water and climatic conditions on the Earth's surface.
