Analýza termodynamických jevů v potrubních sítích – numerický model teplotního pole v okolí teplárenského potrubí – 1. část
Další z řady článků, zabývajících se vyhodnocováním tepelných ztrát teplárenských sítí, se věnuje numerickému modelování teplotního pole v bezprostředním i vzdálenějším okolí povrchu potrubní izolace.
V souvislosti s obtížností řešení analytickými metodami a především v souvislosti s nepřesností jejich výsledků zejména v méně typických, přesto nikoliv vzácných provozních režimech, se nabízí jako vhodná cesta pro popis celého děje vytvoření dvourozměrného modelu teplotního pole vznikající během provozu kolem teplárenského potrubí. Předložený numerický model využívá růstu výpočetních kapacit v posledních letech tak, že velikost jednoho segmentu výpočtové mřížky je 10 × 10 mm, což je, např. pro stanovení vhodnosti umístění jiné potrubní sítě, či kabelu, v okolí horkovodu, jemnost již dostatečná. Vzniklý numerický model je připravován, na rozdíl od podstatné části analytických metod, pro výpočet plného rozsahu možných provozních podmínek horkovodu a klimatických podmínek na zemském povrchu.
Obsah
| Anotace |
| Summary |
| • Obsah |
| Seznam použité symboliky |
| 1. Úvod |
| 1.1. Odborný problém |
| 2. Matematický model |
| 2.1. Stanovení rozsahu výpočtového teplotního pole |
| 2.2. Popis numerické metody |
| 2.2.1. Numerické schéma |
| 2.3. Výsledky numerického řešení teplotního pole okolí potrubí zasypaného v zemním zásypu |
| 3. Hodnocení přesnosti numerického modelu |
| 4. Aplikace numerické modelu teplotního pole pro posouzení vhodnosti souběhu horkovodu s dalšími inženýrskými sítěmi |
| 5. Návrh další diskuse |
| 6. Získané poznatky |
| 7. Seznam použité literatury |
Seznam použité symboliky
| Latinská abeceda | ||
| a | teplotní vodivost (teplotní difusivita) zásypové hmoty | m2/s |
| cp | měrná tepelná kapacita za konstantního tlaku | J/(kg‧K) |
| cv | měrná tepelná kapacita za konstantního objemu | J/(kg‧K) |
| C | osová rozteč potrubí | m |
| d | průměr | m |
| h | hloubka/ výška | m |
| i | pořadové číslo řady | [–] |
| I | izolační konstanta | (m‧K)/W |
| n | pořadové označení | [1] |
| q | měrný tepelný tok vztažený k jednotce délky | W/m |
| r | poloměr | m |
| t | teplota | °C |
| T | absolutní teplota | K |
| x | souřadnice vodorovného směru | m |
| X | celková šířka teplotního polem | |
| y | souřadnice svislého směru | m |
| Y | celková výška teplotního polem | |
| Řecká abeceda | ||
| λ | tepelná vodivost | W/(m‧K) |
| ρ | hustota | kg/m3 |
| τ | čas | s |
| Δ | rozdíl hodnot | |
| Dolní indexy | ||
| 0 | počáteční stav | |
| E | vztaženo k vlastnostem zeminy | |
| f | vztaženo k přívodní linii | |
| iz | vztaženo k vlastnostem izolační hmoty | |
| max | vztaženo k maximální hodnotě | |
| min | vztaženo k minimální hodnotě | |
| r | vztaženo k vratné linii | |
1. Úvod
Vedení tepla v izolovaném potrubí v zemním zásypu je poměrně složitý děj, u něhož analytické řešení, s ohledem na možná zjednodušení, nemusí vždy vést ke spolehlivým výsledkům. V souvislosti s rozvojem výpočetních kapacit je však možno vytvořit poměrně přesný numerický model celého teplotního pole v okolí potrubní trasy a na jeho základě pracovat s hodnotami teplot v této oblasti. Cesta využití numerického modelu umožňuje poměrně podrobné zmapování okolí zdrojů tepla v zemním zásypu, které pak je vodítkem při umisťování další inženýrských sítí v oblasti zasažené tepelným tokem z teplárenských tras.
Obsah teplotního pole podzemního potrubí je dán superpozicí jednotlivých vlivů, z nichž podstatnou část je možno využít jako okrajové podmínky pro numerický model a při modelování jejich změn je pak možno sledovat vývoj tohoto pole v konkrétních situacích, ovlivnitelných provozními režimy potrubních tras, nebo daných přírodními podmínkami. Uvedený postup je testován v této práci na mnoha běžných i hraničních provozních stavech měřeného horkovodu a výsledky analytického řešení, numerického modelu a měření jsou v článku porovnávány.
1.1. Odborný problém
Důvodem, proč uvedená problematika nebyla doposud úspěšně řešena, jsou především nároky na výpočetní kapacitu, dané potřebou hustoty výpočetní sítě řešeného teplotního pole s jeho proměnnými tepelně-technickými vlastnostmi, vstupujícími do každé provedené iterace výpočtu, a především pak obtížná práce v terénu během instalace i v průběhu experimentu. Jedním z možných důvodů, proč v tomto směru byly doposud provedeny pouze dílčí experimenty, byla nutnost dlouhodobé úzké spolupráce s provozovateli horkovodní sítě při dodržení všech platných provozních a bezpečnostních norem a předpisů.
2. Matematický model
Řešení matematického modelu modelu tepelné ztráty dvojice izolovaného potrubí vychází z postupů uvedených v literatuře [1] a [2].
2.1. Stanovení rozsahu výpočtového teplotního pole
Teplotní pole předpokládající konstantní tepelně-technické vlastnosti zásypového materiálu bylo voleno, s ohledem na možnost použití Dirichletových a Neumannových okrajových podmínek, s tím, že podstatnou je volba šířky a výšky teplotního pole tak, aby byly splněny následující podmínky:
Pro celou horní hranu teplotního pole musí platit, že při dostatečně zvolené výšce zásypu potrubí je teplota na povrchu země, a to po celé šířce vyšetřovaného teplotního pole (v rozsahu x = 0 až x = xmax), v daném okamžiku přibližně konstantní, tedy hodnota teplot t(x=0 až xmax) ≅ konst. Jedná se tedy o Dirichletovu okrajovou podmínku, kdy po celé horní hraně teplotního pole známe hodnotu teploty v každém z bodů pro celý průběh výpočtu.
![Obrázek 2.1.1. – Průměrná teplota rostlé zeminy v závislosti na hloubce pod povrchem země a ročním období převzato a přeloženo z [4]](/docu/clanky/0163/016342o2.png)
Obrázek 2.1.1. – Průměrná teplota rostlé zeminy v závislosti na hloubce pod povrchem země a ročním období převzato a přeloženo z [4]
Pro stanovení okrajových podmínek na levém a pravém okraji teplotního pole, je možno uvést, že teplota se, od určité hodnoty vzdálenosti od povrchu topného potrubí, ve vodorovném, tedy x-ovém, směru, již dále nemění, tedy ![]() zatímco ve směru svislém se teplota na levé a pravé hranici teplotního pole mění, a to už jak především v závislosti na povrchové teplotě potrubních plášťů izolace, tak i v závislosti na teplotě na horním okraji teplotního pole (povrchu země), a dále na hloubce od povrchu i na čase (období v roce), tzn. že t = f (t4f, t4r, t0, y, τ) , kde t0 je teplota na povrchu země, a tedy
zatímco ve směru svislém se teplota na levé a pravé hranici teplotního pole mění, a to už jak především v závislosti na povrchové teplotě potrubních plášťů izolace, tak i v závislosti na teplotě na horním okraji teplotního pole (povrchu země), a dále na hloubce od povrchu i na čase (období v roce), tzn. že t = f (t4f, t4r, t0, y, τ) , kde t0 je teplota na povrchu země, a tedy ![]() . Na levém a pravém okraji se tedy jedná o Neumannovy okrajové podmínky.
. Na levém a pravém okraji se tedy jedná o Neumannovy okrajové podmínky.
Spodní okraj vyšetřované oblasti, zde přesněji spodní okraj numericky modelovaného teplotního pole, je z hlediska okrajových podmínek výpočtu řešen tak, že je umístěn v hloubce, ve které je již teplota celoročně přibližně konstantní, tedy se pro žádný okamžik v průběhu činnosti horkovodu nemění. Tedy, pro určitou hloubku y (vzdálenost od zemského povrchu) už platí, že t(x=0 až xmax) = konst. Jedná se o Dirichletovu okrajovou podmínku – známe hodnotu teploty v každém bodě po celé délce spodní hrany teplotního pole. Podrobně je problematika teploty zeminy v jednotlivých hloubkách řešena v např. v [3] a dále se problematikou průběhu teplot v zemi, v závislosti na ročním období, zabývá [4]. Z uvedených údajů je patrné, že se teplota zeminy, v hloubce 4 m pod povrchem země, mění během roku již minimálně a dá se konstatovat, že osciluje kolem střední teploty 8,8 °C s max. rozptylem ±2 °C, jak je patrné z průběhu teplot (viz Obrázek 2.1.1.).
Šířka modelovaného teplotního pole byla volena s ohledem na doporučení obsažená v [5], kdy pro šíření tepla v neomezeném prostoru je možno považovat v případě izolované trubky povrchovou teplotu izolace za izotermu. Ve skutečnosti se však, jak také ostatně vyplývá z naměřených dat, v případě obvodového pláště izolace jedná o kružnici (o průměru rovnou vnějšímu průměru izolačního pláště d4) obsahující po svém obvodu místa s mírně rozdílnými teplotami, kdy na vnějším dolním půlkruží (např. v bodě B) je teplota mírně vyšší, než na jeho horním půlkruží (površce) – např. v bodě A – viz Obrázek 2.1.2. Důvodem je poloha jednotlivých bodů v semihomogenním prostoru.
Pro ustálený stav lze uvést, že v neomezeném prostoru pro neizolované potrubí platí
kde IE je izolační konstanta účinné vrstvy zeminy, t4 je povrchová teplota potrubí a tE je teplota země v příslušné hloubce. Dále platí, že
Za předpokladu stejné teploty ve všech bodech kruhové izotermy, bude i pro všechny její body poměr ![]() Ve skutečnosti se však r2 mění. Při větší hloubce uložení, a při relativně malém průměru izotermy, je tato změna nepatrná a tedy je možno uvažovat přibližně střední hodnotu, tj. r2 ≈ 2r, a pak bude poměr poloměrů
Ve skutečnosti se však r2 mění. Při větší hloubce uložení, a při relativně malém průměru izotermy, je tato změna nepatrná a tedy je možno uvažovat přibližně střední hodnotu, tj. r2 ≈ 2r, a pak bude poměr poloměrů
Z uvedeného plyne, že
![Obrázek 2.1.4. – Stanovení rozsahu oblasti zasažené změnou teploty způsobenou dvěma zdroji tepla v zemině dle [5]](/docu/clanky/0163/016342o15.png)
Obrázek 2.1.4. – Stanovení rozsahu oblasti zasažené změnou teploty způsobenou dvěma zdroji tepla v zemině dle [5]
Tento vzorec lze graficky interpretovat i tak, že účinná vrstva zeminy, mající vliv na výpočet tepelných ztrát, sahá k okruhu o průměru 4h.
Z uvedeného a další argumentace uvedené v [5] je možno usoudit, že celková šířka tepelně ovlivněné oblasti v zemním zásypu nepřesáhne, zejména v případě použití tepelné izolace, čtyřnásobek vzdálenosti mezi osou potrubí a povrchem země h – viz Obrázek 2.1.4.
Uvedené závěry dle [5] jsou platné pro geometrické podmínky, kdy povrch potrubí, nebo povrch jeho izolace, je vzdálen od povrchu země více než 0,7 m při současně platícím poměru h / d4 > 1,25, což naprostá většina, především horkovodních tras, včetně té, která byla předmětem měření a výpočtů popsaných v tomto článku, splňuje. V souladu s uvedenými údaji je možno předpokládat, že celková šířka tepelně ovlivněné oblasti ve směru x bude o velikosti X = 4h, tedy cca 5,1 m. Vzhledem k tomu, že se v posuzovaném případě jedná o 2 potrubí umístěná vedle sebe s osovou roztečí C = 0,43 m, lze předpokládat rozšíření této ovlivněné oblasti nejméně o tuto hodnotu osové rozteče. Tedy byla za účelem stanovení šířky teplotního pole, a jejího vybavení správnými okrajovými podmínkami pro numerický výpočet, zvolena šířka zájmové oblasti ve směru x, tedy ve směru kolmém na osy potrubí a rovnoběžném s povrchem země (viz Obrázek 2.1.5.), o rozměru x600–x0 = 6000 mm. Silná tmavá čára uvnitř řešeného teplotního pole v Obrázku 2.1.5. vymezuje oblast montážního výkopu, jedná se o hlinito-písčitou hmotu, která je během instalace horkovodu vyjmuta ze země, a po doplnění pískových vrstev do bezprostředního okolí potrubí je pak, za trvalého hutnění, ve své většině, navrácena zpět.
Na základě jednoho z cílů této práce – stanovení možnosti tepelného ovlivnění dalších inženýrských sítí v okolí provozované horkovodní trasy, byla poté stanovena hlavní zájmová oblast s vysokou hustotou teplotních čidel. Touto oblastí je především bezprostřední okolí předizolované trubní konstrukce v pískovém zásypu ve vzdálenosti do 1 m od nejbližší površky izolačního pláště potrubí a oblast mezi povrchem země a povrchy izolace těchto potrubí, což je oblast, kde lze předpokládat nejvyšší změnu teploty způsobenou provozem horkovodního potrubí.
V průběhu měření a jeho následné interpretaci v konkrétních hodnotách tepelné vodivosti hlinito-písčitého zásypu však bylo zjištěno, že jeden z původních předpokladů pro tvorbu matematického modelu, tedy, že tepelná i teplotní vodivost okolí potrubí je konstantní, nebyl zcela správný, neboť hlinito-písčitý zásyp má, především z technologických důvodů, rozdílný obsah písku v hlíně v rozpětí od 10 do 95 %, a tedy i proměnnné tepelně-technické vlastnosti. Tyto rozdíly vlastností lze, alespoň přibližně, vyjádřit formou proměnné hodnoty teplotní vodivosti aE = f (x,y), a to tak, aby se rozprostření teplotní i tepelné vodivosti v modelovém prostoru co nejvíce podobalo obvyklé tepelně-technické situaci v okolí zasypané trubní konstrukce.
Článek pokračuje v dalším dílu
Another of several articles dealing with thermal losses evaluation of heating networks is focused on the numerical modeling of the temperature field in the immediate and distant surroundings of the pipe insulation surface. In connection with the difficulty of solving the analytical methods and in particular with the inaccuracy of their results, especially in less typical but not rare operating regimes, a two-dimensional model of the thermal field generated during the operation around the heating pipeline is offered as a suitable path for describing the whole process. The presented numerical model uses the growth of computational capacities in recent years, so that the size of one segment of the calculation grid is 10 × 10 mm, which is, for example, to determine the suitability of the location of another pipe network or cable, near the hot-water pipe, the fineness is already sufficient. The resulting numerical model is being prepared, unlike a substantial part of the analytical methods, to calculate the full range of possible operating conditions of the hot-water and climatic conditions on the Earth's surface.

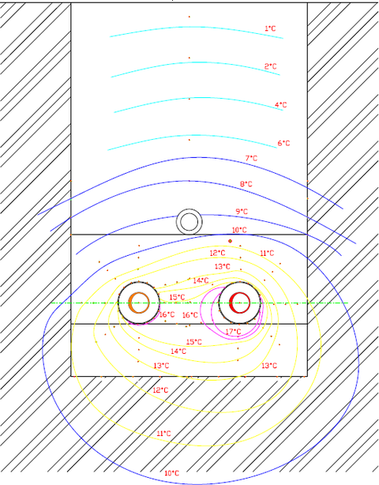
![Obrázek 2.1.2. – Izotermy v okolí potrubí v zemním zásypu, překresleno a upraveno dle [5]](/docu/clanky/0163/016342o6.png)